分岐数の平均
趣旨
ひたすら繰り返して行えば、全棋譜数の近似値が出そうだという証明が出たので実験してみました。
実験時間は家を空けている間ということで、timeコマンドによると603分かけてます。
方針
1手:分岐数を数え、その中から一様乱数で一つを選択する。
1回:↑の作業をゲーム終了分まで続け、終了までの分岐数の積を取ります。
全体:家を空けている間↑を繰り返して、平均(相加平均)を取りました。
多少はデータの分散状況も見たかったので10万回ごとの平均も取ってます。
吐き出したデータ
統計データのファイルは…not supported って言われたんで、下記のリンクから
見て下さい。sim.txt と sim.dat (同じデータです。一方を消したいけど方法が分からん)
ついでなんでプログラムソースもUploadしました。sim.c.txt参照。
形式の説明を兼ねて一部(形式を変えて(※))書いておきます。
「最近10万回の平均」とは例えば最後の行で言えば3億6950万1回目から3億6960万回目までの10万回の平均です。
実験回数 最近10万回の平均 全体の平均 // ←この行はデータ内にありません
: : :
36920万 6.53832313e+54 6.4495692838e+54
36930万 6.23481340e+54 6.4495111317e+54
36940万 6.79935358e+54 6.4496058373e+54
36950万 6.53681788e+54 6.4496294400e+54
36960万 6.25990966e+54 6.4495781089e+54
※そのまま書くとなぜか妙な形になったので。
最後の部分だけ書くと、3億6960万回の平均で
6,449,578,108,875,017,297,533,965,593,363,280,821,664,540,000,000,000,000
になりましたが、その前(3億6950万回)の出力と比較すると有効数字は4桁くらいですね。
ということで、こんなに頑張っても 6.449×10^54 あたりではなかろうか、というのが限界です。
グラフ
分散状況が分かりやすい(はずだった)グラフは
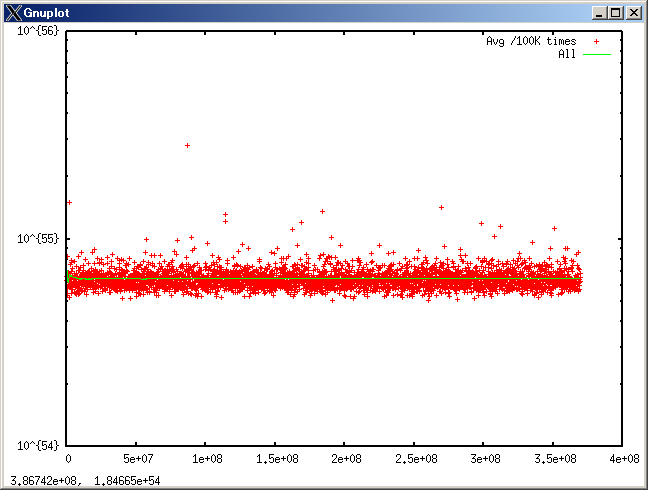
こんなんなりました。
赤い十字(に見えないくらい多いけど)が10万回ごとの平均、緑の線がそれまでの全てで取った平均を表しています。
大雑把に言えば、極まれに外れ値がある、と。統計データはご自分で出すか私が出すのをゆったりお待ち下さい。
最終更新:2006年03月09日 22:44